
As in previous editions, emphasis is placed on methods commonly seen in kinesiology, such as correlation and bivariate regression, t tests, analysis of variance (ANOVA), and the interpretation of interactions in factorial analyses of variance. The fifth edition also incorporates fully updated content reflecting the changing face of kinesiology:
- Comparisons of observational versus experimental research and nonparametric versus parametric methods of analyzing categorical and ordinal data
- More detailed coverage on how to calculate central tendency when data have been transformed (e.g., log transformations) as well as multiple ways to interpret the correlation coefficient
- Expanded coverage of statistical graphs, including dot plots and spaghetti plots
- A discussion of the real meaning of p values and confidence intervals
- An introduction to frequentist approaches versus Bayesian methods
Statistical software tools commonly used in kinesiology applications—such as JASP and G*Power—are briefly introduced, encouraging students to apply their knowledge of statistical procedures to generate and interpret computer results with confidence and ease.
With Statistics in Kinesiology, Fifth Edition, students will gain a solid understanding of the statistical techniques used in physical activity fields. The book’s practical approach, based on the authors’ more than 50 years of combined experience in teaching statistics, will make it easy for students to learn these important, but often intimidating, concepts.
What Is Measurement?
Process of Measurement
Variables and Constants
Research Design and Statistical Analysis
Statistical Inference
Summary
Chapter 2. Organizing and Displaying Data
Organizing Data
Displaying Data
Summary
Chapter 3. Percentiles
Common Percentile Divisions
Calculations Using Percentiles
Summary
Chapter 4. Measures of Central Tendency
Mode
Median
Mean
Relationships Among the Mode, Median, and Mean
Summary
Chapter 5. Measures of Variability
Range
Interquartile Range
Variance
Standard Deviation
Definition Method of Hand Calculations
Calculating Standard Deviation for a Sample
Coefficient of Variation
Standard Deviation and Normal Distribution
Summary
Chapter 6. The Normal Curve
Z Scores
Standard Scores
Probability and Odds
Calculating Skewness and Kurtosis
Summary
Chapter 7. Fundamentals of Statistical Inference
Predicting Population Parameters Using Statistical Inference
Estimating Sampling Error
Levels of Confidence, Confidence Intervals, and Probability of Error
An Example Using Statistical Inference
Statistical Hypothesis Testing
Type I and Type II Error
Degrees of Freedom
Living With Uncertainty
Two- and One-Tailed Tests
Applying Confidence Intervals
Summary
Chapter 8. Correlation and Bivariate Regression
Correlation
Calculating the Correlation Coefficient
Bivariate Regression
Homoscedasticity
Summary
Chapter 9. Multiple Correlation and Multiple Regression
Multiple Correlation
Partial Correlation
Multiple Regression
Summary
Chapter 10. The t Test: Comparing Means From Two Sets of Data
The t Tests
Types of t Tests
Magnitude of the Difference (Size of Effect)
Determining Power and Sample Size
The t Test for Proportions
Summary
Chapter 11. Simple Analysis of Variance: Comparing the Means Among Three or More Sets of Data
Assumptions in ANOVA
Sources of Variance
Calculating F: The Definition Method
Determining the Significance of F
Post Hoc Tests
Magnitude of the Treatment (Size of Effect)
Summary
Chapter 12. Analysis of Variance With Repeated Measures
Assumptions in Repeated Measures ANOVA
Calculating Repeated Measures ANOVA
Correcting for Violations of the Assumption of Sphericity
Post Hoc Tests
Interpreting the Results
An Example From Leisure Studies and Recreation
Summary
Chapter 13. Quantifying Reliability
Intraclass Correlation Coefficient
Standard Error of Measurement
Summary
Chapter 14. Factorial Analysis of Variance
A Between–Between Example
A Between–Within Example
A Within–Within Example
Summary
Chapter 15. Analysis of Covariance
Relationship Between ANOVA and Regression
ANCOVA and Statistical Power
Assumptions in ANCOVA
The Pretest–Posttest Control Group Design
Pairwise Comparisons
Summary
Chapter 16. Analysis of Nonparametric Data
Chi-Square (Single Classification)
Chi-Square (Two or More Classifications)
Rank Order Correlation
Mann-Whitney U Test
Kruskal-Wallis ANOVA for Ranked Data
Friedman’s Two-Way ANOVA by Ranks
Summary
Chapter 17. Clinical Measures of Association
Relative Risk
Odds Ratio
Diagnostic Testing
Summary
Chapter 18. Advanced Statistical Procedures
Multilevel Modeling
Meta-Analysis
Multiple Analysis of Variance
Factor Analysis
Discriminant Analysis
Summary
Appendix: Statistical Tables
Joseph P. Weir, PhD, is the chair of the department of health, sport, and exercise sciences at the University of Kansas. From 1995 to 2012 he was a professor in the physical therapy doctorate program at Des Moines University in Iowa. He earned his doctorate in exercise physiology from the University of Nebraska at Lincoln.
Weir is a fellow of both the American College of Sports Medicine (ACSM) and the National Strength and Conditioning Association (NSCA). He was given the NSCA President’s Award in 2007 and its William J. Kraemer Outstanding Sport Scientist Award in 2006. He served as president of the National Strength and Conditioning Association Foundation from 2006 to 2009, and he was cochair of the ACSM’s Biostatistics Interest Group from 2001 to 2003.
Weir is a senior associate editor of the Journal of Strength and Conditioning Research, and he is a member of the editorial board of Medicine and Science in Sports and Exercise. He is the author of numerous research articles, which have appeared in European Journal of Applied Physiology, Physiological Measurement, American Journal of Physiology, and Journal of Orthopaedic and Sports Physical Therapy. He is coauthor of Physical Fitness Laboratories on a Budget, and he has contributed chapters to seven texts, including NSCA’s Essentials of Personal Training.
Weir is originally from Glennallen, Alaska. He and his wife, Loree, live in Lawrence, Kansas, and have three adult children. He is an avid motorcyclist and a fan of University of Nebraska football, University of Kansas basketball, and Boston Bruins hockey.
William J. Vincent, EdD, is a retired adjunct professor and former director of the general education wellness program in the department of exercise sciences at Brigham Young University in Provo, Utah. He is a professor emeritus and the former chair of the department of kinesiology at California State University at Northridge (CSUN). He was employed at CSUN for 40 years and taught statistics and measurement theory for 35 of those years. In 1995 he received the university’s Distinguished Teaching Award.
Vincent has been a member of the American Alliance for Health, Physical Education, Recreation and Dance (AAHPERD), now SHAPE America, since 1964. In 2007, he received the AAHPERD National Honor Award for distinguished service to the profession. He has served as the president of the Southwest District of AAHPERD and was a member of the AAHPERD board of governors from 1993 to 1995. In 1988 he was named the Southwest District Scholar and delivered the keynote address, titled "From Means to MANOVA," at the 1989 convention.
Vincent is the author or coauthor of four books and more than 70 professional articles. Fifty-one of those articles appeared in refereed journals, including Research Quarterly for Exercise and Sport, International Journal of Sports Medicine, and Journal of Athletic Training. He has a bachelor’s degree in physical education (pedagogy), a master’s degree in physical education (exercise physiology), and a doctorate in educational psychology (perception and learning), all from the University of California at Los Angeles.
Vincent lives in Lindon, Utah. He and his late wife, Diana, raised six children, and he has 24 grandchildren and nine great-grandchildren. In his free time, he enjoys camping, snow skiing and water skiing, conducting genealogical research, and reading.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
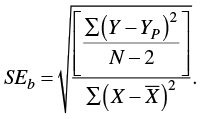 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
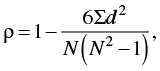 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.
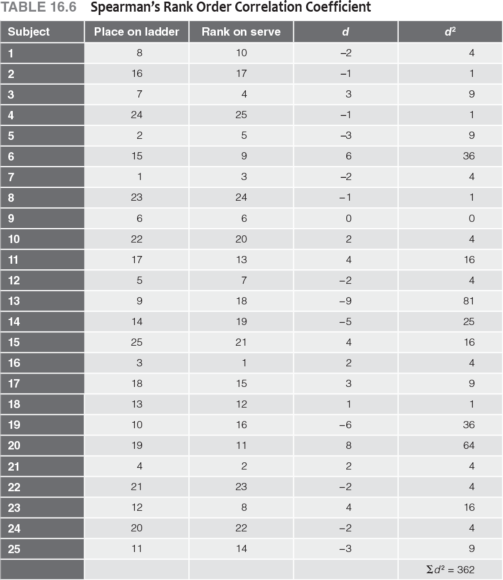
When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
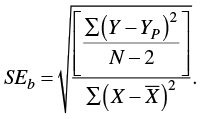 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
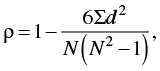 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
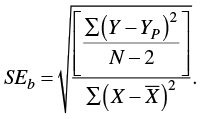 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
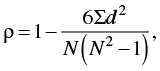 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
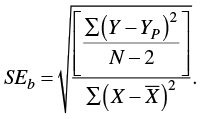 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
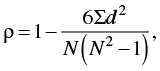 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
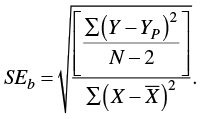 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
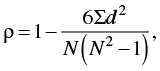 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
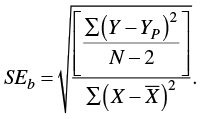 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
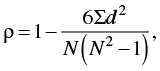 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
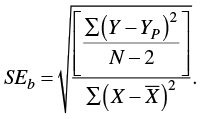 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
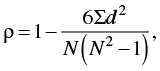 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
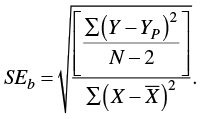 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
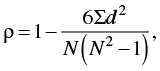 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.
Standard error of measurement
The intraclass correlation coefficient provides an estimate of the relative error of the measurement; that is, it is unitless and is sensitive to the between-subjects variability. Because the general form of the intraclass correlation coefficient is a ratio of variabilities (see equation 13.04), it is reflective of the ability of a test to differentiate between subjects. It is useful for assessing sample size and statistical power and for estimating the degree of correlation attenuation. As such, the intraclass correlation coefficient is helpful to researchers when assessing the utility of a test for use in a study involving multiple subjects. However, it is not particularly informative for practitioners such as clinicians, coaches, and educators who wish to make inferences about individuals from a test result.
For practitioners, a more useful tool is the standard error of measurement (SEM; not to be confused with the standard error of the mean). The standard error of measurement is an absolute estimate of the reliability of a test, meaning it has the units of the test being evaluated and is not sensitive to the between-subjects variability of the data. Further, the standard error of measurement is an index of the precision of the test, or the trial-to-trial noise of the test. Standard error of measurement can be estimated with two common formulas. The first formula is the most common and estimates the standard error of measurement as
![]() (13.06)
(13.06)
where ICC is the intraclass correlation coefficient as described previously and SD is the standard deviation of all the scores about the grand mean. The standard deviation can be calculated quickly from the repeated measures ANOVA as
![]() (13.07)
(13.07)
where N is the total number of scores.
Because the intraclass correlation coefficient can be calculated in multiple ways and is sensitive to between-subjects variability, the standard error of measurement calculated using equation 13.06 will vary with these factors. To illustrate, we use the example data presented in table 13.5 and ANOVA summary from table 13.6. First, the standard deviation is calculated from equation 13.07 as
![]()
Recall that we calculated ICC (1,1) = .30, ICC (2,1) = .40, and ICC (3,1) = .73. The respective standard error of measurement values calculated using equation 13.07 are
![]() for ICC (1,1),
for ICC (1,1),
![]() for ICC (2,1),
for ICC (2,1),
and
![]() for ICC (3,1).
for ICC (3,1).
Notice that standard error of measurement value can vary markedly depending on the magnitude of the intraclass correlation coefficient used. Also, note that the higher the intraclass correlation coefficient, the smaller the standard error of measurement. This should be expected because a reliable test should have a high reliability coefficient, and we would further expect that a reliable test would have little trial-to-trial noise and therefore the standard error should be small. However, the large differences between standard error of measurement estimates depending on which intraclass correlation coefficient value is used are a bit unsatisfactory.
Instead, we recommend using an alternative approach to estimating the standard error of measurement:
![]() (13.08)
(13.08)
where MSE is the mean square error term from the repeated measures ANOVA. From table 13.6, MSE = 1,044.54. The resulting standard error of measurement is calculated as
![]()
This standard error of measurement value does not vary depending on the intraclass correlation coefficient model used because the mean square error is constant for a given set of data. Further, the standard error of measurement from equation 13.08 is not sensitive to the between-subjects variability. To illustrate, recall that the data in table 13.7 were created by modifying the data in table 13.1 such that the between-subjects variability (larger standard deviations) was increased but the means were unchanged. The mean square error term for the data in table 13.1 (see table 13.2, MSE= 1,070.28) was unchanged with the addition of between-subjects variability (see table 13.8). Therefore, the standard error of measurement values for both data sets are identical when using equation 13.08:
![]()
Interpreting the Standard Error of Measurement
As noted previously, the standard error of measurement differs from the intraclass correlation coefficient in that the standard error of measurement is an absolute index of reliability and indicates the precision of a test. The standard error of measurement reflects the consistency of scores within individual subjects. Further, unlike the intraclass correlation coefficient, it is largely independent of the population from which the results are calculated. That is, it is argued to reflect an inherent characteristic of the test, irrespective of the subjects from which the data were derived.
The standard error of measurement also has some uses that are especially helpful to practitioners such as clinicians and coaches. First, it can be used to construct a confidence interval about the test score of an individual. This confidence interval allows the practitioner to estimate the boundaries of an individual's true score. The general form of this confidence interval calculation is
T = S ± Zcrit (SEM), (13.09)
where T is the subject's true score, S is the subject's score on the test, and Zcrit is the critical Z score for a desired level of confidence (e.g., Z = 1.96 for a 95% CI). Suppose that a subject's observed score (S) on the Wingate test is 850 watts. Because all observed scores include some error, we know that 850 watts is not likely the subject's true score. Assume that the data in table 13.7 and the associated ANOVA summary in table 13.8 are applicable, so that the standard error of measurement for the Wingate test is 32.72 watts as shown previously. Using equation 13.09 and desiring a 95% CI, the resulting confidence interval is
T = 850 watts ± 1.96 (32.72 watts) = 850 ± 64.13 watts = 785.87 to 914.13 watts.
Therefore, we would infer that the subject's true score is somewhere between approximately 785.9 and 914.1 watts (with a 95% LOC). This process can be repeated for any subsequent individual who performs the test.
It should be noted that the process described using equation 13.09 is not strictly correct, and a more complicated procedure can give a more accurate confidence interval. For more information, see Weir (2005). However, for most applications the improved accuracy is not worth the added computational complexity.
A second use of the standard error of measurement that is particularly helpful to practitioners who need to make inferences about individual athletes or patients is the ability to estimate the change in performance or minimal difference needed to be considered real (sometimes called the minimal detectable change or the minimal detectable difference). This is typical in situations in which the practitioner measures the performance of an individual and then performs some intervention (e.g., exercise program or therapeutic treatment). The test is then given after the intervention, and the practitioner wishes to know whether the person really improved. Suppose that an athlete improved performance on the Wingate test by 100 watts after an 8-week training program. The savvy coach should ask whether an improvement of 100 watts is a real increase in anaerobic fitness or whether a change of 100 watts is within what one might expect simply due to the measurement error of the Wingate test. The minimal difference can be estimated as
![]() (13.10)
(13.10)
Again, using the previous value of SEM = 32.72 watts and a 95% CI, the minimal difference value is estimated to be
![]()
We would then infer that a change in individual performance would need to be at least 90.7 watts for the practitioner to be confident, at the 95% LOC, that the change in individual performance was a real improvement. In our example, we would be 95% confident that a 100-watt improvement is real because it is more than we would expect just due to the measurement error of the Wingate test. Hopkins (2000) has argued that the 95% LOC is too strict for these types of situations and a less severe level of confidence should be used. This is easily done by choosing a critical Z score appropriate for the desired level of confidence.
It is not intuitively obvious why the use of the ![]() term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
term in equation 13.10 is necessary. That is, one might think that simply using equation 13.09 to construct the true score confidence interval bound around the preintervention score and then seeing whether the postintervention score is outside that bound would provide the answer we seek. However, this argument ignores the fact that both the preintervention score and the postintervention score are measured with error, and this approach considers only the measurement error in the preintervention score. Because both observed scores were measured with error, simply observing whether the second score falls outside the confidence interval of the first score does not account for both sources of measurement error.
We use the ![]() term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here,
term because we want an index of the variability of the difference scores when we calculate the minimal difference. The standard deviation of the difference scores (SDd) provides such an index, and when there are only two measurements like we have here, ![]() We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by
We can then solve for the standard deviation of the difference scores by multiplying the standard error of measurement by ![]() . Equation 13.10 can be reconceptualized as
. Equation 13.10 can be reconceptualized as
MD = SDd × Zcrit.
As with equation 13.09, the approach outlined in equation 13.10 is not strictly correct, and a modestly more complicated procedure can give a slightly more accurate confidence interval. However, for most applications the procedures described are sufficient.
An additional way to interpret the size of the standard error of measurement is to convert it to a type of coefficient of variation (CoV). Recall from chapter 5 that we interpreted the size of a standard deviation by dividing it by the mean and then multiplying by 100 to convert the value to a percentage (see equation 5.05). We can perform a similar operation with the standard error of measurement as follows:
![]() (13.11)
(13.11)
where CoV = the coefficient of variation, SEM = the standard error of measurement, and MG = the grand mean from the data. The resulting value expresses the typical variation as a percentage (Lexell and Downham, 2005). For the example data in table 13.7 and the associated ANOVA summary in table 13.8, SEM = 32.72 watts (as shown previously) and MG = 774.0 (calculations not shown). The resulting CoV = 32.72/774.0 × 100 = 4.23%. This normalized standard error of measurement allows researchers to compare standard error of measurement values between different tests that have different units, as well as to judge how big the standard error of measurement is for a given test being evaluated.
Statistical significance and confidence intervals for bivariate regression
Earlier in this chapter we showed how to test for the statistical significance of the Pearson r and that we can construct a confidence interval about the r value. We can also test whether the regression equation is statistically significant and can construct a confidence interval about the slope coefficient (b) from the regression analysis. As it turns out, for bivariate regression the test of the significance of r and the significance of b is redundant. If r is significant, the regression equation is significant. However, we address the process here because it will help you understand the workings of multiple regression, which is addressed in chapter 9.
To test the statistical significance of b and calculate the confidence interval about b, we use a test statistic called t. The t statistic, which is somewhat analogous to a Z score, is examined in more detail in chapter 10, where techniques to examine differences between mean values are introduced. However, the t statistic is useful for more than just comparing means. The t statistic is based on a family of sampling distributions that are similar in shape to the normal distribution, except the tails are thicker than a normal distribution. When sample sizes are small, the t distributions more accurately reflect true probabilities than does the normal distribution.
When we test the statistical significance of b, we are testing whether the slope coefficient is significantly different from zero. (We can also test whether b differs from some hypothesized value other than zero, but this is rarely done in kinesiology.) The statistical hypotheses for a two-tailed test are as follows:
H0: b = 0
H1: b ≠ 0.
The degrees of freedom for the test are n − 2. The test statistic t for this analysis is calculated as (Lewis-Beck, 1980):
![]() (8.14)
(8.14)
where b is the slope coefficient and SEb is the standard error of b. We calculate the standard error of b as
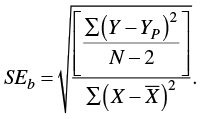 (8.15)
(8.15)
Notice what this equation is telling us. Inside the radical, the numerator is reflecting how much error is in the predictions, because we are adding up the squared differences between the actual Y scores and the predicted Y scores (once again a sums of squares calculation) and dividing it by a degrees of freedom term (a sort of mean square because we are taking a sum and dividing it by a degrees of freedom term). The denominator is the sums of squares for X, the independent variable. The better the prediction of Y based on X, the smaller will be the standard error of b. The smaller the standard error of b, the larger will be the t statistic, all else being equal. The larger the t statistic, the less tenable is the null hypothesis.
Fortunately, most of the work in this calculation has been done already in table 8.3. Substituting the appropriate terms into equation 8.15, we get
![]()
To calculate t, we substitute the appropriate values into equation 8.14 so that
![]()
To determine the statistical significance of t, we can use table A.3a in the appendix. To be statistically significant at a two-tailed α = .05 and with df = 13, the calculated t must be ≥ 2.16. Because 5.71 > 2.16, we can reject H0 and conclude that the number of push-ups is a significant predictor of isometric time to failure. Recall that t is analogous to Z but is used in cases of small sample sizes. Table 7.1 on page 72 shows that a Z score of 1.96 corresponds with a 95% LOC (two-tailed). With 13 df, the 95% LOC (two-tailed) corresponds to a t value of 2.16. The t value associated with the 95% LOC value (2.16) is larger than the Z value associated with the 95% LOC value, which is reflective of the thicker tails of the t distribution relative to the normal distribution. Examine table A.3a for the two-tailed data under the .05 α level. Notice that as the degrees of freedom get larger, the tabled values for t get smaller so that at df = ∞, the values for t and Z are equal. That is, as the degrees of freedom increase, the t distribution approaches a normal distribution. (One can consider the normal distribution as just a special case of the t distribution with infinite degrees of freedom.)
We also use the t distribution to calculate a confidence interval about the slope coefficient. The confidence interval is calculated as
![]() (8.16)
(8.16)
where t is the critical t value from table A.3a for a given α and degrees of freedom. For the push-up data, the t value we need (95% LOC, df = 13) is once again 2.16. Previously, we determined that b = .726 and SEb = 0.127. Therefore, the 95% CI for the push-up data is
.726 ± (2.16)(0.127) = 0.45 to 1.00.
In a journal, we might report this as b = 0.726 seconds per push-up, 95% CI = 0.45, 1.00. Thus, we are 95% confident that the population slope lies somewhere from 0.45 and 1.00 seconds per push-up. Notice that zero is not inside the 95% CI, which means that the slope is statistically significant (p < .05).
In practice, these calculations are rarely performed by hand. They are too cumbersome and it is easy to make arithmetic errors. In addition, at each step rounding error will occur. Statistical software performs these calculations faster and more accurately. Plus, statistical software will generate actual p values that are more precise than those generated from looking values up in a table and reporting, for example, p < .05. Nonetheless, seeing where the numbers come from is useful in developing an understanding of how these tests work.
Sample Size
Ideally, the sample size of a study using correlation and bivariate regression should be determined before the start of the study. Free and easy to use software known as G*Power is available to perform these calculations. G*Power can be downloaded from www.gpower.hhu.de/en.html, and Faul and colleagues (2009) have described how to use the software for sample size calculations with correlation and bivariate regression studies. The primary decisions an investigator must make in this situation are defining the smallest effect that would be of interest and deciding what level of statistical power is desired. For example, assume we determine that the smallest correlation of interest between number of push-ups and time to failure (see table 8.3) is .30. That is, we decide that any correlation less than .30 is too small to be of interest. In addition, we choose a power level of 80% (or 0.80). From G*Power, if we set the correlation to .30 and set α to .05 and power = 0.80, we would need to test 84 subjects. Instead, if we set the smallest correlation of interest to .40 and left the α at .05 and power at 0.80, then only 46 subjects would be necessary. In contrast, if we left the minimal interest to be r = 0.30 and α = .05 but increased the desired power to 0.90, we would need to test 112 subjects.
What is rank order correlation?
Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.
Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is
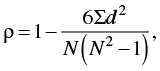 (16.04)
(16.04)
where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.
The degrees of freedom for ρ are the same as for Pearson's r: df = Npairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.
An Example From Physical Education
We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.
The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:
![]()
Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H0 is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.
Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.










